Bayes Test for One
Proportion
Home | Academic Articles
Contrast of frequentist vs. Bayesian
approach
Suppose
we have a salesperson who has the following track record over a 3-week period:
|
|
Number
of sales calls |
Number
of sales |
|
Week
1 |
5 |
1 |
|
Week
2 |
5 |
0 |
|
Week
3 |
5 |
5 |
|
Total |
15 |
6 |
If
the goal is to have the sales rate exceed 20%, can we conclude at a 5% level of
significance that the goal is being achieved?
The null and alternative
hypotheses are:
Ho: p < 20%
Ha:
p > 20%
From
a frequentist point of view, the p-value is the probability of having at least
6 sales in the 15 trials. If p = 20%, P(X >
6) = 1 – P(X < 5) = 1 – 0.939 = 0.061 = 6.1%. Since 6.1% > 5%, we
do not reject the null hypothesis and conclude that the goal is not being
achieved.
From
a Bayesian point of view, the p-value can be viewed as the probability of the
null hypothesis being true.
For
the prior distribution of p, we can assume that it can uniformly take any value
between 0 and 1. Thus, f(p) = 1.
Since
we have 6 successes and 9 failures, the posterior distribution of p is
proportional to p6(1 – p)9. This indicates that p follows a Beta
distribution with α = 7 and β = 10. Thus, when we solve for P(p < 0.2), we get:
Once
you work through the math, P(p < 0.2) is equivalent
to the probability of having at least 7 successes in 16 trials given p = 0.2.
This works out to 0.0267 = 2.67%. Since 2.67% < 5%, we reject the null
hypothesis and conclude the goal is being achieved.
Asymptotic results
Suppose the null and alternative
hypotheses are changed to:
Ho: p < 40%
Ha:
p > 40%
From
the frequentist point of view, the p-value = P(X >
6) = 1 – P(X <
5) = 1 – 0.403 = 0.597 = 59.7%. From the Bayesian point of view, the p-value = P(p < 0.4) which is equivalent to the probability of at
least 7 successes in 16 trials given p = 0.4. This works out to 0.4728 = 47.28%.
Now,
the sample proportion (
= 6/15 = 0.4. For various values of n and p,
we want to find the probability of the null hypothesis being true.
|
n
| p |
0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
|
15 |
2.67% |
47.28% |
77.28% |
94.17% |
99.29% |
99.98% |
100% |
|
50 |
0.04% |
48.48% |
91.96% |
99.78% |
100% |
100% |
100% |
|
100 |
0 |
48.92% |
97.7% |
100% |
100% |
100% |
100% |
|
500 |
0 |
49.51% |
100% |
100% |
100% |
100% |
100% |
|
1000 |
0 |
49.66% |
100% |
100% |
100% |
100% |
100% |
For
p < 40%, as n increases, P(Ho being true) decreases
and eventually reaches a probability of zero for all intents and purposes.
However,
if p = 40%, as n increases, P(Ho being true)
approaches 50%.
Finally,
for p > 50%, as n increases, P(Ho being true)
increases and eventually reaches a probability of 100% for all intents and
purposes.
These
probabilities are roughly comparable to p-values from the frequentist school.
For example, if p = 0.2, n = 100 and 
= 0.4, the value of the
test statistic would be:
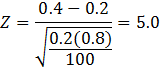
The
p-value = P(Z > 5) = 0 for all intents and
purposes.
If
p = 0.4 and = 0.4, Z = 0 regardless
of the sample size and P(Z > 0) = 0.5.
Finally,
if p = 0.5, n = 100 and = 0.4, the value of the
test statistic would be:
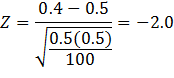
The
p-value = P(Z > -2) = 97.73%.
Jeffrey’s non-informative prior with test
for p
If
Jeffrey’s non-informative prior is used, α = x and β = n – x. In the
first example with n = 15 and x = 6, the posterior distribution of p is proportional to p5(1
– p)8.
Given the null and
alternative hypotheses:
Ho: p < 20%
Ha:
p > 20%
P(p < 20%) is equivalent to the probability
of having at least 6 successes in 14 trials given p = 0.2. This works out to 0.0439
= 4.39%.
In
general, P(Ho being true) = P(p < po) = 1 – P(X < x-1 | n-1, po) in which po
represents the hypothesis proportion.
If
x = n, P(Ho being true) = 1 – P(X < n-1 |
n-1, po) = 1 – 1 = 0.
Thus,
Jeffrey’s non-informative prior cannot be used for hypothesis testing. This is
also due to the fact that P(p) = 1/[p(1-p)] is not a proper PDF as illustrated
here:
Let
u = 1 – p. Then du = -dp.
The
result is undefined since ln(0) is negative infinity.
Reference:
Zellner, Arnold. An Introduction to Bayesian Inference in
Econometrics. New York: John Wiley & Sons, 1970.