![]()
Confidence
Intervals and Two-tailed Hypothesis Testing for Means
Home | Academic Articles
The basics
In Bayesian analysis, the population mean
(μ) is a random variable with its own mean and standard deviation. If we
have a confidence interval for a mean, the theory states that for a random
sample of 100 means drawn from the same population, we would expect 95 of them
to fall inside the confidence interval. This allows us to use a confidence
interval to determine whether or not to reject the null hypothesis for a
two-tailed hypothesis test.
Example
Suppose we have these null and alternative
hypotheses:
Ho: μ = 100
Ha: μ ≠ 100
We collect a random sample of 100 values and
find that the sample mean is 102.5 and the standard deviation is 8.5.
If we test at a 5% level of significance, the
critical values are 1.96 and -1.96. As explained in the technical details, the
area between these critical values corresponds to the 95% confidence interval
for μ. But, this is also the acceptance region of the test in which we do
not reject the null hypothesis. Thus, if the hypothesis mean of 100 falls
inside the 95% confidence interval, we do not reject the null hypothesis at a
5% level of significance. Otherwise, we reject the null hypothesis.
Given the data, we construct the 95%
confidence interval:
![]()
![]()
![]()
Since μ = 100 falls outside the 95% confidence
interval, we reject the null hypothesis at a 5% level of significance.
This principle can also be applied to the t
test for means.
Suppose we have the same sample mean and
standard deviation as in the last example but the sample size is now 10. If we
test at a 5% level of significance, the critical values are 2.262 and -2.262
(based on 9 degrees of freedom).
We construct the 95% confidence interval:
![]()
![]()
![]()
Since μ = 100 falls inside the 95%
confidence interval, we do not reject the null hypothesis at a 5% level of
significance.
Technical details
We have the null and alternative hypotheses:
Ho: μ = μ0
Ha: μ ≠ μo
If we test at a 5% level of significance, we
do not reject the null hypothesis if the test statistic falls between the
critical values of 1.96 and -1.96.
If this is a Z test, the test statistic is:
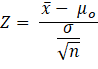
Substituting the formula for Z, we do not
reject the null hypothesis if:
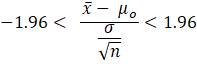
Solving for μo gives the
following results:
![]()
![]()
The term at the left end of the inequality is the
lower limit of the 95% confidence interval while the term at the right end is
the upper limit. Thus, we do not reject the null hypothesis at a 5% level of
significance if the hypothesis mean falls inside the 95% confidence interval.
The same logic applies to the t test; we
simply replace the Z critical values with the corresponding t critical values
and replace the population standard deviation (σ) with the sample standard
deviation (s).