The basics
A
normal distribution has two parameters, the mean
which indicates where the bell curve is
centered and
the standard deviation 
which indicates the shape of the bell curve. From a frequentist point of view, and are fixed quantities. From a Bayesian point of
view, they are random variables each with their own distribution, mean and
standard deviation.
If
a researcher has a set of data that appears to follow a normal distribution, we
would like to find the distributions of and .
If
the researcher does not have a clear idea as to what distribution and jointly follow, Jeffreys
suggested a diffuse prior distribution to indicate this lack of knowledge. When
this prior distribution is combined with the data (known as the likelihood),
the joint posterior distribution of and does not follow any readily identifiable
distribution.
However,
once we solve for just from the joint posterior distribution, we find
that it follows a t distribution with the mean equal to 
which represents the sample mean of the data
and the variance equal to
in which 
represents the sample standard deviation of
the data. Note that the sample size needs to be more than 3 in order to have a
standard deviation. The other thing to note is that as the sample size
increases, the standard deviation of gets closer to zero.
Similarly,
once we solve for just from the joint posterior distribution, we find
that it follows an inverse gamma distribution with the mean equal to
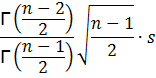
where 
is the gamma function of x. To have a mean,
the sample size needs to be more than 1. The variance is
To
derive the standard deviation, we take the square root of the above quantity.
To have a standard deviation, the sample size needs to be more than 3.
Example
Suppose
a researcher takes a sample of 10 observations of people buying gas at a
service station:
|
39.62 |
48.21 |
52.48 |
57.06 |
57.24 |
|
60.04 |
63.64 |
68.05 |
73.98 |
81.24 |
Analysis
indicates the data is normally distributed.
We
have = 60.16, = 12.2545, 
= 150.17 and 
= 10.
The
posterior distribution of indicates it follows a t distribution with a
mean of 60.16 and variance of (9/7)(150.17/10) =
19.3078 or a standard deviation of 4.39 with 9 degrees of freedom.
Employing
Chebyshev’s theorem, at least 8/9 of the distribution lies between 60.16 –
3(4.39) = 46.99 and 60.16 + 3(4.39) = 73.33.
The
posterior distribution of follows an inverse gamma distribution with a
mean of
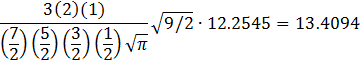
The
variance is
The
standard deviation is then the square root of 13.2663 which is 3.64.
Employing
Chebyshev’s theorem, at least 8/9 of the distribution lies between 13.41 – 3(3.64)
= 2.49 and 13.41 + 3(3.64) = 24.33.
Then,
returning to the distribution of X, we can construct a table indicating the
range of 
depending on their values:
|
μ |
σ |
2.49 |
13.41 |
24.33 |
|
46.99 |
(39.52,
54.46) |
(6.76,87.22) |
(0,
119.98) |
|
60.16 |
(52.69,
67.63) |
(19.93,
100.39) |
(0,
133.15) |
|
73.33 |
(65.86,
80.80) |
(33.10,
113.56) |
(0.34,
146.32) |
Of
these ranges, the one with μ = 60.16 and σ = 13.41 seems the most
plausible. As more data is added, the range of μ and σ will tighten up.
For example, I generated 1000 normal random numbers with a mean of 60.16 and
standard deviation of 13.41. The mean of the data is 60.21 and the sample
variance is 182.0687. Based on this data, μ follows a t distribution with
a mean of 60.21 and standard deviation of 0.43 and σ follows an inverse
gamma distribution with a mean of 13.50 and standard deviation of 0.30.
Technical details
If
the researcher is starting from scratch, the joint prior distribution of and should convey this. The suggestion made by
Jeffreys is to have
.
Since
our data appears to follow a normal distribution, each value y follows this distribution:
Given
the random sample 
, the likelihood
function is:
where represents the sample mean of the data.
The
expression 
is derived as follows:
The
first term is derived from the fact that 
.
There
is no middle term from FOIL since 
.
Then
Posterior Distribution of μ
To
derive the posterior distribution of , we integrate 
with respect to .
We
use the substitution 
in which 
represents the degrees of freedom. The result
is:
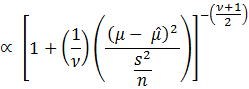
Thus,
follows a t distribution.
If
we let
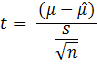
then
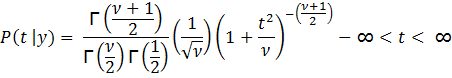
where is the gamma function
of x.
To
find the mean of t, E(t | y), we have:
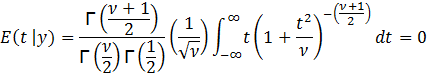
This
follows since 
is an odd function of t. From that we derive 
and consequently 
provided > 1. Note that if = 1, the integral does not provide a finite
solution. (In fact, t would follow a Cauchy distribution.)
Since
E(t) = 0, the variance of t, Var(t)
= E(t2)
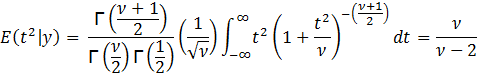
Since
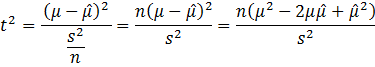
then
This
follow from the previous derivation of 
.
Then,
This
indicates that as the sample size increases, the variance of decreases.
Posterior Distribution of σ
To
derive the posterior distribution of , we integrate with respect to .
We
use the substitution . The result is:
This
is in the form of an inverse Gamma distribution. Thus,
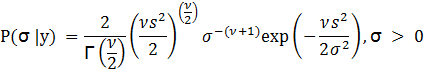
In
this case, 
and 
.
To
find the mean of σ, E(σ | y), we have:
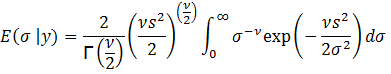
Let
y = 1/σ2. Then σ2 = y-1 leading to
σ = y-0.5 and dσ = -0.5y-1.5
dy. Substituting, we get:
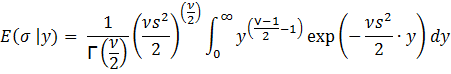
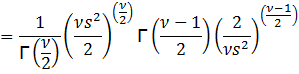
The
last line follows from the equation for the gamma function:
Then,
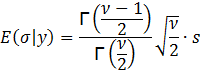
To
find the variance of σ, we need E(σ2
| y):
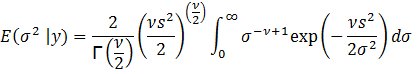
Again,
let y = 1/σ2. Then σ = y-0.5 and dσ = -0.5y-1.5 dy. Substituting, we get:
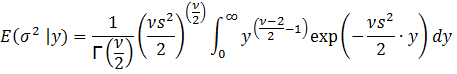
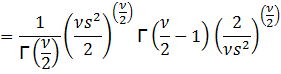
Then
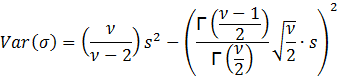
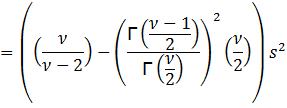
Thus,
we need > 2 in order to have a variance and
subsequently a standard deviation.
Reference:
Zellner, Arnold. An Introduction to Bayesian
Inference in Econometrics. New York: John Wiley & Sons, 1970.